What is intensity?
Sound waves are characterized by compression and expansion of the medium as sound energy moves through it. This represents the pressure component of sound. At the same time, there is also back and forth motion of the particles making up the medium (particle motion).
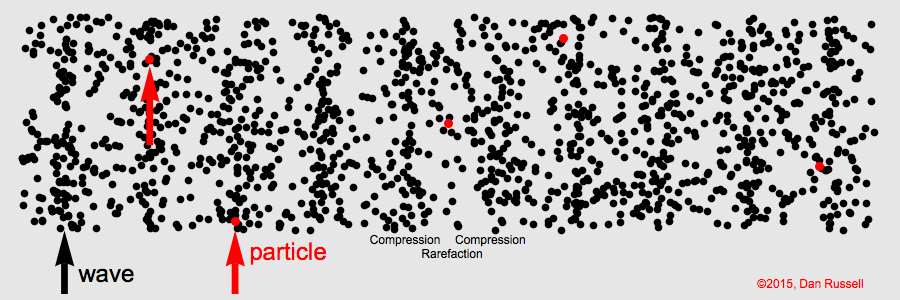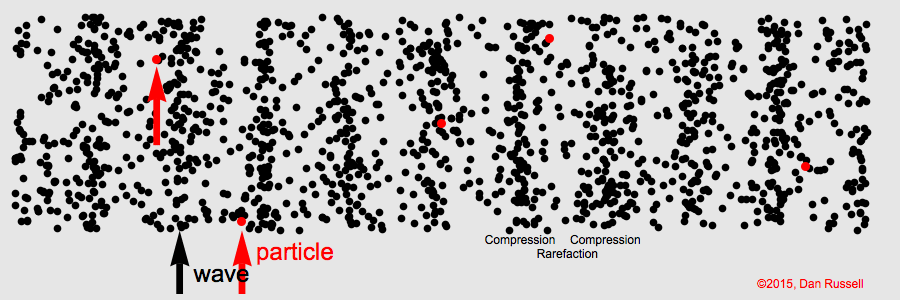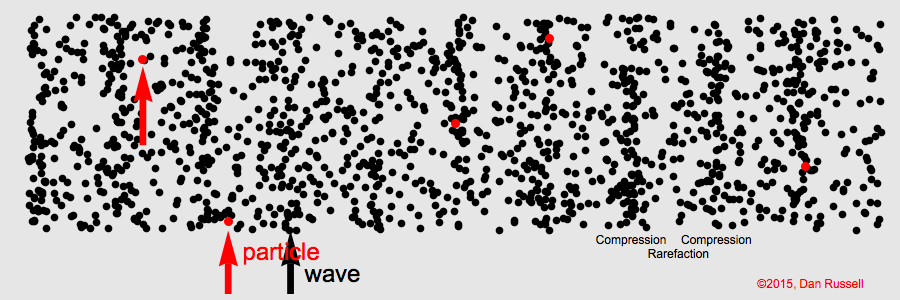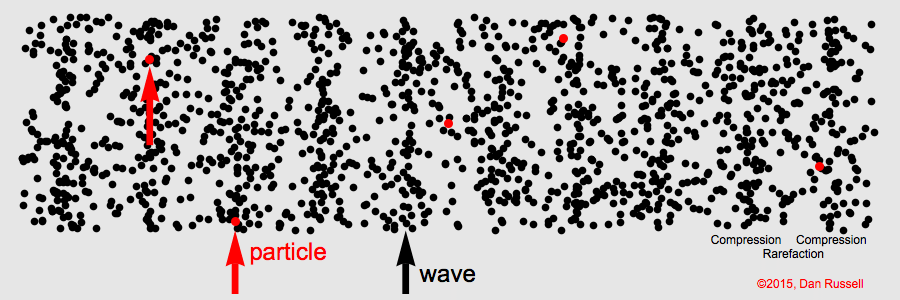
Sound is a longitudinal wave. Animation credit: Dan Russell, Grad. Prog. Acoustics, Penn State, https://www.acs.psu.edu/drussell/Demos/waves/wavemotion.html
Particle motion is described by displacement, velocity, and acceleration.
The intensity of a sound wave is defined as the amount of energy transmitted through a unit area per unit time in the direction in which the sound wave is traveling. The energy transmitted by a sound wave is comprised by both pressure (potential energy due to the acoustic impedance) and particle velocity (kinetic energy due to the movement of the particles) components. Thus sound intensity depends on both particle velocity and pressure. It is given by the product of the pressure and velocity of the sound wave:
intensity ( ), pressure (p), particle velocity (
)
The arrow over the symbol for particle velocity indicates that velocity is a vector quantity; i.e., it has both a magnitude and direction. The motion of particles in a sound wave generally align with the direction in which the wave is traveling. Pressure, on the other hand, does not have a direction associated with it.
The ratio of acoustic pressure (p) to the associated particle speed in a medium (u) is called the specific acoustic impedance (z).
z = p/u
For plane waves propagating in the + x direction, this ratio is:
z = ρo c
Because density (ρo) and sound speed (c) are characteristics of the medium such water or air, the ρoc is often called the characteristic impedance of the medium. For air at standard temperature and pressure, the characteristic impedance is ρoc = 415 Pa s/m. For fresh water at 20° C and 1 atm, the characteristic impedance is ρoc = 1.48 x106 Pa s /m. These numbers indicate that water and air have very different impedances, which alters the relationship between intensity, pressure, and particle speed for a sound wave inside each medium.

Diagram of a plane wave. The red rectangles represent wavefronts of a plane wave traveling in three-dimensional (3-D) space.
Using the previous equation, particle velocity for a plane wave can be written as a function of pressure, density, and sound speed:
The intensity ( ) of a plane wave therefore depends not only on the pressure (p), but also on the density (ρ ) and sound speed (c ) of the medium through which the sound is traveling:
Sounds in water and sounds in air that have the same pressures have very different intensities because the impedance of water is much greater than the impedance of air. For the same pressure, the higher density and higher sound speed of water results in a lower intensity, because the particle velocity in water is much lower than that in air. The difference in impedance of air and water means that sound waves with the same pressure will have intensity levels that differ by 35.5 dB. The reference levels in air (20 mPa rms) and water (1 mPa rms) result in another 26 dB, so that a plane wave with the same pressure in air and water will have intensities (sound pressure levels) that differ by 35.5+26 = 61.5 dB.
Put another way, a plane wave in air has larger particle velocity than a sound wave of equivalent pressure propagating through water, because the lower density of air makes it easier to accelerate quickly. So even though both waves share the same pressure, the higher particle velocity in the airborne wave generates a higher intensity.
The most common device for measuring underwater sound is a hydrophone. Hydrophones measure the pressure (amplitude) of a sound wave, rather than its intensity. Hydrophones are not sensitive to particle velocity. The sound intensity level is therefore calculated from the measured sound pressure, using the relationship between the magnitude of the intensity and pressure. (For more detail, see: Introduction to Decibels)
Geophones measure particle velocity, but are more commonly used to measure seismic waves than underwater sound waves. Vector sensors measure particle velocity or acceleration together with pressure to provide direct measurements of intensity, including the direction in which the sound wave is traveling. Vector sensors are used in DIFAR (Directional Frequency Analysis and Recording) sonobuoys, for example.
Additional Links on DOSITS
- Science of Sound > What is sound?
- Science of Sound > How do you characterize sounds?
- Science of Sound > How fast does sound travel?
- Science of Sound > How does sound in air differ from sound in water?
- Science of Sound > Introduction to Decibels (Advanced Topic)
- Science of Sound > How does sound move? Wave Propagation and Huygens’ Principle (Advanced Topic)
- Animals and Sound > What components of sound are used for hearing? (Advanced Topic)
- Animals and Sound > How do marine mammals hear?
- Animals and Sound > How do fish hear?
- Technology Gallery > Geophone
- Technology Gallery > Vector Sensors
- Technology Gallery > Hydrophone/Receiver
- Technology Gallery > Sonobuoys
References
- Dr. Dan Russell, Graduate Program in Acoustics, Penn State, Longitudinal and Transverse Wave Motion.