Individual-specific Vocalizations
Many cetacean species have highly developed communication systems to establish or maintain contact with group members. Among the best studied of these vocalizations are the signature whistles of bottlenose dolphins. Each bottlenose dolphin has a unique signature whistle used to broadcast the animal’s identity and location.

A pod of Indo-Pacfic bottlenose dolphins. Image credit: S. Dukachev.
During the first year of life, a dolphin develops its signature whistle based upon other whistles in its environment (“vocal learning”). Once developed, the dolphin’s signature whistle usually does not change significantly. The figure below shows 3 repetitions of a relatively simple dolphin signature whistle, with a frequency sweep from 7 kHz to 23 kHz.
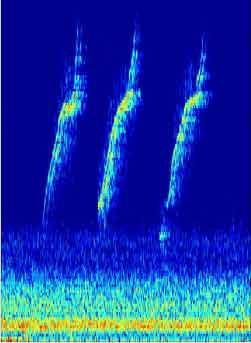
This is a spectrogram of a bottlenose dolphin whistle. Time is shown in seconds on the x-axis. Frequency in kilohertz is plotted on the y-axis and increases in pitch as the numbers increase. The static in the lower portion of the image is lower frequency noise in the background of the recording. (Courtesy of Jennifer L. Miksis Olds).
Bottlenose dolphin whistle recorded at Mystic Aquarium while the dolphin was isolated in a side pool.
Sound clip provided by Jennifer L. Miksis Olds. Released under Creative Commons License, non-commercial – no derivs.
Below are three examples of more complex signature whistles from other dolphins (Courtesy of Jennifer Miksis-Olds).
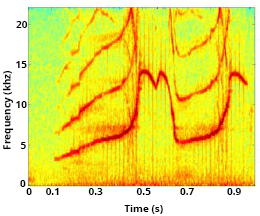
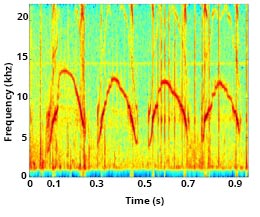
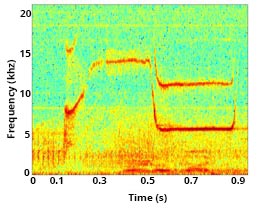
Signature whistles have been recorded in several contexts. For example, dolphins produce their signature whistles when groups meet at sea, or, in captivity, when an individual is separated from a group. In addition, dolphins occasionally mimic the signature whistles of other dolphins with which they have close social bonds, such as mother/calf pairs or male-male pairs.
In addition to bottlenose dolphins, there is evidence that other dolphin species including Atlantic spotted dolphins, Pacific white-sided dolphins, and Pacific humpback dolphins, also produce signature whistles. Beluga whales and narwhals may also produce individually distinct vocalizations.
Sperm whales produce rhythmic patterns of clicks when they are resting or socializing at the surface. These clicks are much shorter than dolphin whistles and have a much broader frequency. They sound very similar to a loud human handclap. The click patterns are called codas. It is common to hear whales exchange codas during social behaviors. It was originally thought that codas were individually distinctive; however, many studies have found this not to be the case. It turns out the situation with codas is much more complex (see group specific vocalizations), but there is some evidence that certain coda types may have individually distinctive features, such as interpulse intervals.
Below is a recording (and associated spectrogram) of sperm whale codas. The sound clip contains the same coda used three times in succession by a single sperm whale off Hawaii. The spectrogram shows the patterned sets of clicks that make up the coda. Note the timing of the click sequence within a single coda – the interval of time between the first and second clicks is longer than the time between the second and third click. The timing of the clicks in the sequence is what makes each coda pattern unique.
This is a recording of sperm whale codas. The sound clip contains the same coda used three times in succession by a single sperm whale off Hawaii. The spectrogram shows the patterned sets of clicks that make up the coda. Note the timing of the click sequence within a single coda – the interval of time between the first and second clicks is longer than the time between the second and third click. The timing of the clicks in the sequence is what makes each coda pattern unique. The sperm whale coda was recorded near Hawaii. Sound courtesy of WhaleAcoustics, LLC.
Additional Links on DOSITS
- Beluga Whale
- Bottlenose Dolphin
- Common Dolphin
- Group-specific Vocalizations
- Narwhal
- Sperm Whale
- White-sided Dolphin
References
- Caldwell, M. C., & Caldwell, D. K. (1965). Individualized whistle contours in bottle-nosed dolphins (Tursiops truncatus). Nature, 207(4995), 434–435. https://doi.org/10.1038/207434a0
- Caldwell, M. C., & Caldwell, D. K. (1971). Statistical evidence for individual signature whistles in the Pacific whitesided dolphin, Lagenorhynchus obliquidens. Cetology, 3, 1–9.
- Caldwell, M. C., Caldwell, D. K., & Miller, J. F. (1973). Statistical evidence for individual signature whistles in the spotted dolphin, Stenella plagiodon. Cetology, 16, 1–21.
- Clausen, K. T., Wahlberg, M., Beedholm, K., Deruiter, S., & Madsen, P. T. (2011). Click communication in harbour porpoises Phocoena phocoena. Bioacoustics, 20(1), 1–28. https://doi.org/10.1080/09524622.2011.9753630
- Dawson, S. M. (2010). Clicks and communication: The behavioural and social contexts of Hector’s dolphin vocalizations. Ethology, 88(4), 265–276. https://doi.org/10.1111/j.1439-0310.1991.tb00281.x/li>
- Fripp, D., Owen, C., Quintana-Rizzo, E., Shapiro, A., Buckstaff, K., Jankowski, K., … Tyack, P. (2005). Bottlenose dolphin (Tursiops truncatus) calves appear to model their signature whistles on the signature whistles of community members. Animal Cognition, 8(1), 17–26. https://doi.org/10.1007/s10071-004-0225-z
- Janik, V. M. (2009). Acoustic Communication in Delphinids. In Advances in the Study of Behavior (Vol. 40, pp. 123–157). Elsevier. https://doi.org/10.1016/S0065-3454(09)40004-4
- Janik, V. M., & Sayigh, L. S. (2013). Communication in bottlenose dolphins: 50 years of signature whistle research. Journal of Comparative Physiology A, 199(6), 479–489. https://doi.org/10.1007/s00359-013-0817-7
- King, S. L., Sayigh, L. S., Wells, R. S., Fellner, W., & Janik, V. M. (2013). Vocal copying of individually distinctive signature whistles in bottlenose dolphins. Proceedings of the Royal Society B: Biological Sciences, 280(1757), 20130053–20130053. https://doi.org/10.1098/rspb.2013.0053
- Morisaka, T., Yoshida, Y., Akune, Y., Mishima, H., & Nishimoto, S. (2013). Exchange of “signature” calls in captive belugas (Delphinapterus leucas). Journal of Ethology, 31(2), 141–149. https://doi.org/10.1007/s10164-013-0358-0
- Shapiro, A. D. (2006). Preliminary evidence for signature vocalizations among free-ranging narwhals ( Monodon monoceros ). The Journal of the Acoustical Society of America, 120(3), 1695–1705. https://doi.org/10.1121/1.2226586
- Tyack, P. L. (1999). Communication and Cognition. In J. E. I. Reynolds & S. A. Rommel (Eds.), Biology of Marine Mammals (pp. 287–323). Washington D.C.: Smithsonian Institution Press.
- Tyack, P. L. (2000). Functional Aspects of Cetacean Communication. In J. Mann, R. C. Connor, P. L. Tyack, & H. Whitehead (Eds.), Cetacean Societies: Field Studies of Dolphins and Whales (pp. 270–307). Chicago, IL: University of Chicago Press.
- Watwood, S. L., Tyack, P. L., & Wells, R. S. (2004). Whistle sharing in paired male bottlenose dolphins, Tursiops truncatus. Behavioral Ecology and Sociobiology, 55(6), 531–543. https://doi.org/10.1007/s00265-003-0724-y