Introduction to Phase
What is Phase?
An important characteristic of a sound wave is the phase. Phase specifies the location or timing of a point within a wave cycle of a repetitive waveform. Typically, it is the phase difference between sound waves that is relevant, rather than the actual absolute phases of the signals. When two sound waves are added, for example, the difference between the phases of the two waves is important in determining the resulting waveform.
The phase difference between two sound waves of the same frequency moving past a fixed location is given by the time difference between the same positions within the wave cycles of the two sounds (the peaks or positive-going zero crossings, for example), expressed as a fraction of one wave cycle.
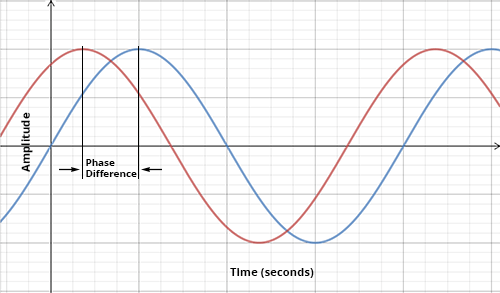
Two waveforms with an arbitrary phase difference
Two sound waves of the same frequency that are perfectly aligned have a phase difference of 0 and are said to be “in phase.” Two waves that are in phase add to produce a sound wave with an amplitude equal to the sum of the amplitudes of the two waves. This process is called “constructive interference.”
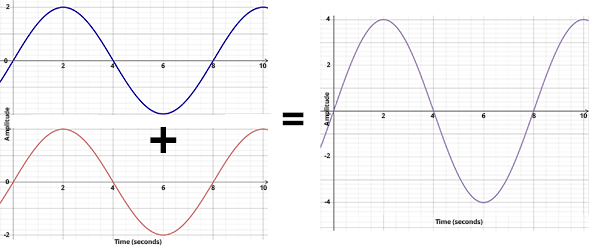
Two sound waves that are in phase add to produce a sound wave of greater amplitude. Credit DOSITS.
If one of the two sound waves of the same frequency is shifted by one-half cycle relative to the other, so that one wave is at its maximum amplitude while the other is at its minimum amplitude, the sound waves are said to be “out of phase.” Two waves that are out of phase exactly cancel each other when added together. This principle, which is used in noise-cancelling headphones, is called “destructive interference.” Both constructive and destructive interference explain many properties of sound in the ocean.

Two sounds waves whose phases differ by one-half cycle exactly cancel when added together. Credit DOSITS.
A short DOSITS video about phase.
A phase difference is normally expressed in terms of an angle, rather than as a fraction of a wave cycle. The phase difference can be described as an angle because the waveform of a pure tone consisting of a single frequency can be represented with the trigonometric sine function (which is why it is called a “sine wave”):
y(t) = A sin(2 π f t)
where y(t) is the waveform, A is the amplitude, f is the frequency (hertz or cycles/second), and t is time (seconds). In this equation the argument of the sine function (2 π f t) is an angle expressed in radians, with π=3.14159… The sine wave is periodic, consisting of wave cycles that repeat over time, as shown in the following figure.
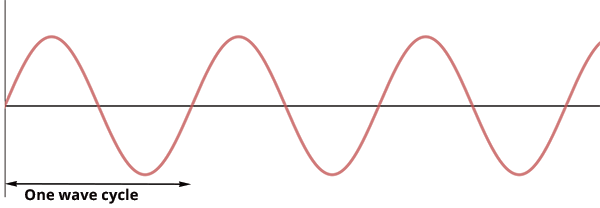
The values of sin(2 πft) as a function of time over one full cycle are:
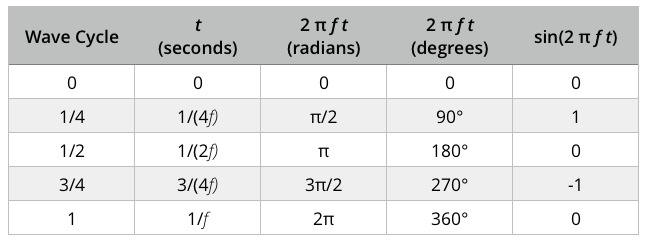
The locations on a wave cycle can therefore be specified as an angle in either radians or degrees, as well as in fractions of a cycle. This can be visualized with a rotating wheel and a spoke tracing the sine wave.
DOSITS animation illustrating phase angle and a sine wave.
Most sounds are much more complex than a single frequency, consisting of many different sine waves at different frequencies and phases. When more than one sine wave combines to create a sound, the waveforms of all the sine waves combine together at each location along the waveform. Any sound can be completely described by the amplitude and phase of its sine wave component at every frequency. Most computer programs that model how a particular sound propagates in the ocean must compute how both the amplitude and phase of each frequency component alters as it travels.
Humpback whale songs can be typically heard in their winter breeding grounds (e.g., Hawaii), but this recording of a humpback whale singing was actually taken in one of their feeding grounds on Cordell Bank Canyon, off the coast of San Francisco, CA. The echoes you hear are from their sounds bouncing off the canyon walls.
Sound ©Thomas R. Kieckhefer. Released under Creative Commons License, non-commercial attribution.
The phase of a sound varies not only over time, but also over space. A full description of a one-dimensional propagating sound tone must account for both the time at which the measurement occurs and the position of the receiver:
y(t) = A sin(2 π f t- 2 π x/λ)
where x is the location of the receiver along a measurement axis, and λ represents the wavelength of the tone. Thus, the same sound measured at two different locations at the same time will also show a phase difference. Similar formulas are used to describe how the phase of a sound varies across three-dimensional space.
Hydrophone arrays use the relative differences in the signal phases received at two or more receivers at different positions (but at the same time) to determine the direction of the source of the signals, a process called beamforming. Projector arrays use the difference in the phases of signals transmitted by two or more projectors to control the direction in which the sound is most intense.
Additional Links on DOSITS
- Science of Sound > Frequency
- Science of Sound > Amplitude (Intensity)
- Science of Sound > Wavelength
- Technology Gallery > Hydrophone Arrays
- Technology Gallery > Projector Arrays
- Technology Gallery > Hydrophone/Receiver
Additional Resources
- Wikipedia: Sine Wave
- Wikipedia: Phase (waves)
- Indiana University, Introduction to Computer Music, What is Phase?
- HyperPhysics – Phase