Introduction to Signal Levels
Sounds travels as a wave. The amplitude of the wave is related to the amount of acoustic energy it carries, or how loud the sound will appear to be. As the amplitude of the sound wave increases, the sound is perceived to be louder. There are several different ways to describe the amplitude of a sound wave. It is important to be aware of the different methods for characterizing the loudness of a sound signal and how they differ from each other. Not all sounds are the same type of wave, and some ways of characterizing a sound wave are more appropriate than others depending on the type of wave. This section will describe the different ways in which a sound wave can be characterized.
The following diagram shows the three most common ways of characterizing the loudness of a sound signal. The two simplest ways of characterizing a sound wave are by its peak pressure and by its peak-to-peak pressure. The peak pressure, also called the 0-to-peak pressure, is the range in pressure between zero and the greatest pressure of the signal. The peak-to-peak pressure is the range in pressure between the most negative pressure and the most positive pressure of the signal. A more complex way of characterizing a sound wave is the root-mean-square pressure. The root-mean-square pressure (abbreviated as rms pressure) is the square root of the average of the square of the pressure of the sound signal over a given duration.
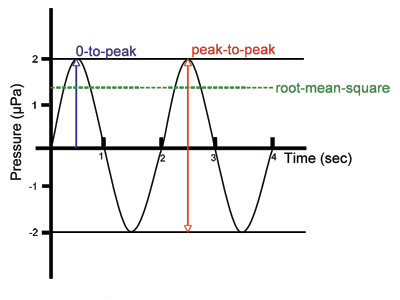
Figure 1: A simple sound wave and three common methods used to characterize the loudness of a sound signal. Image credit: DOSITS.
The root-mean-square pressure is most often used to characterize a sound wave because it is directly related to the energy carried by the sound wave, which is called the intensity. The intensity of a sound wave is the average amount of energy transmitted per unit time through a unit area in a specified direction. The intensity I of a sound wave is proportional to the average over time of the square of its pressure p (See Introduction to Decibels):
(“ρ” is the density of medium carrying the sound and c is the speed of sound). The density and sound speed are relatively constant, and so the intensity is directly related to the mean square pressure:
The root-mean-square (rms) pressure is then just the square root of this:
To calculate the rms pressure, there are four steps. First, the pressure of the sound is measured at points along the sound signal. The pressure is then squared each time it is measured. All of these measurements are averaged (added together and divided by the number of measurements). Finally, the square root of the average of the squared pressures is taken to give the rms pressure of the sound signal. The steps for calculating the rms pressure of the signal shown in the following diagram is given in the table below.

Figure 2: Simple Sound Wave. Image credit: DOSITS.
| Steps for calculating rms pressure | Sample calculation |
| 1. Measure the pressure at points along the sound signal. | 0, 2, 0, -2, 0, 2, 0, -2 |
| 2. Square the measured pressures. | 0, 4, 0, 4, 0, 4, 0, 4 |
| 3. Average the squared pressures. | (0+4+0+4+0+4+0+4)/8 = 2 |
| 4. Take the square root of the average of the squared pressures. | √2 = 1.4 |
There can be significant differences between the three ways of characterizing pressure, peak, peak-to-peak, and rms. This can result in a serious misunderstanding of the magnitude of a signal. The following figure illustrates that each of the methods for describing the pressure of the signal gives a different value. The peak pressure value is 2 μPa, the peak-to-peak pressure value is 4 μPa, and the rms pressure of the signal is 1.4 μPa.

Figure 3: Simple Sound Wave. Image credit: DOSITS.
The rms pressure is most often used to characterize sound waves that have the simple shape shown in the above figures. Not all sound waves have such simple shapes, which contain only one frequency (See How are sound viewed and analyzed?). The situation becomes more complicated when the sound signal is a short impulsive signal, such as sound waves generated by a lightning strike or an airgun. It is easy to estimate the peak-to-peak and peak pressures in these cases, but it becomes more difficult to calculate the rms pressure.

Figure 4: Impulsive Sound Signal. Image credit: DOSITS.
The rms method requires the scientist to select a duration over which to average the pressure of the signal. This method is appropriate for tones in which the average pressure can be directly related to the intensity of the sound signal. It is not appropriate to use rms pressure to measure impulsive sounds, since the rms pressure will vary dramatically depending on the duration over which the signal is averaged. In fact, the longer the time duration over which the signal is averaged, the lower the rms value will be. This is illustrated in the following figure, where the rms pressure is calculated using three different durations for an impulsive signal.
| Duration over which signal is averaged | rms pressure |
| 0.5 sec | 1.4 µPa |
| 1 sec | 1.0 µPa |
| 2 sec | 0.8 µPa |

Figure 5: Impulsive Sound Signal. Image credit: DOSITS.
This can be compared to the peak-to-peak pressure of 3.75 μPa and the 0-to-peak pressure of 2 μPa for the same signal. These methods for characterizing a signal do not depend on the duration of the signal.
The appropriate way in which to characterize a sound wave depends on the question being asked. For example, in order to evaluate the effect of a sound on marine mammals, it is important to describe the sound correctly. Because marine (and other) mammal ears are sensitive to the intensity of a sound wave, the rms pressure is therefore appropriate to use when discussing hearing. The risk of impulsive sound causing physical damage to the ears of a marine mammal depends in part on the peak pressure, which is therefore one of the ways in which impulsive sounds should be characterized.
Sound pressures are often given as relative pressures in units called decibels, The sound pressure is compared to a reference pressure, using the following equation:
The relative pressure in decibels for a sound signal can take on different values depending on the method used to characterize the pressure of the signal. For underwater sounds the reference pressure preference is an rms pressure of 1 μPascal. This is why the units for decibels are given as “dB re1 μPa,” indicating that the reference pressure is 1 μPa rms. If the sound pressure psound used is the rms pressure of a sound wave containing a single frequency, then this equation gives the relative intensity, I, in decibels of the sound wave (See Introduction to Decibels). When other methods for characterizing the pressure of the sound wave, such as peak pressure or peak-to-peak pressure, are used, the result is not the relative intensity of the signal, but the relative pressure. The following table lists decibel values that have all been computed for the same sound signal, which is given in the previous figure.
| Pressure | Decibels |
| rms (0.5 sec): 1.4 µPa | 2.9 dB re 1 µPa |
| rms (1 sec): 1.0 µPa | 0 dB re 1 µPa |
| rms (2 sec): 0.8 µPa | -1.9 dB re 1 µPa |
| 0-to-peak: 2 µPa | 6 dB re 1 µPa |
| peak-to-peak: 3.75 µPa | 11.4 dB re 1 µPa |
The decibel levels in this example range from -1.9 dB re 1 μPa to 11.4 dB re 1 μPa, even though they are all describing the same signal. If the threshold of hearing were 5 dB re 1 μPa, one could conclude either that the sound would be inaudible or would be heard, depending on which value is used.
In addition to stating the reference pressure, it is just as important to tell whether the pressure being used to compute decibels is root-mean-square (rms), peak, or peak-to-peak pressure. There can be significant differences between these measures of signal level, resulting in a serious misunderstanding of the magnitude of a signal if the pressure being used is not specified. On this website, we use underwater dB to indicate decibels computed using root-mean-square pressure, unless otherwise indicated. For situations in which the peak pressure is used, the unit of dB peak will be indicated. If the peak-to-peak pressure is used, the unit of dB peak-peak will be indicated.
Additional Resources
- St. Andrews University, U.K.: Varying signals
- TVTechnology.com: Inside Audio: Levels
References
- Madsen, P. T. (2005). Marine mammals and noise: Problems with root mean square sound pressure levels for transients. The Journal of the Acoustical Society of America, 117(6), 3952–3957. https://doi.org/10.1121/1.1921508
- Chapman, D. M. F., & Ellis, D. (1998). The elusive decibel: Thoughts on sonars and marine mammals. Canadian Acoustics, 26(2), 29–31.